🌟 Understanding the Difference between Suboptimal and Global Optimal Solutions in Flight Crew...
Quantum Computers Cannot Overcome Dzhanibekov Effect
People usually think that optimization is the very problem for quantum computers to solve. Once, we met a team of professionals (who became our mutual friends later) striving to develop an aircrew scheduling application using a quantum computer. Probably you know that I found Rosterize to build an AI that generates and optimizes crew schedules, so we decided to find out if quantum computers could solve optimization problems.
When solving optimization problems, two primary properties matter: linearity and unimodality. Having at least one of these makes the job much easier to cope with.
Here, we’ll talk about unimodality, which means that there is one minimum, both global and local, at the same time. In this case, all we need to do is simply move down the function (this is called gradient descent – something we will need a bit later, so keep it in mind), and – sooner or later – we will find this minimum.
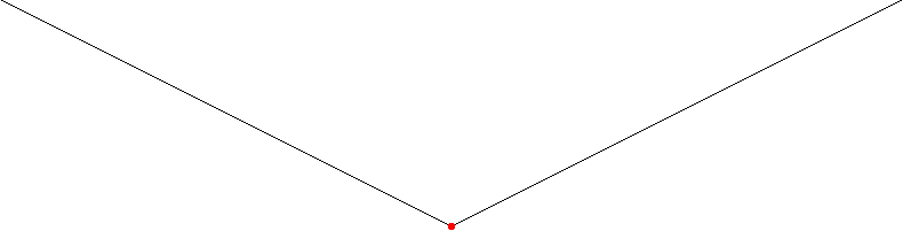
The simplest optimization job.
Linear optimization problems feature both unimodality and linearity, which is why linear optimization is so effective. And the well-known simplex method is in fact, a step-by-step gradient descent. Moreover, gradient descent is the basis for all optimization algorithms.
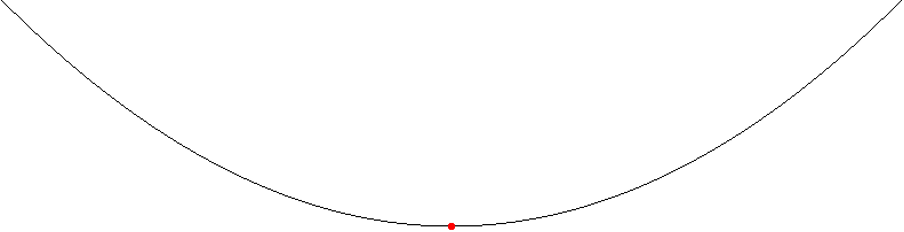
A more difficult problem: one minimum, but a non-linear job.
Practical optimization problems, including crew scheduling, have many local minima. The main challenge here is to get out of the local minimum and continue the same gradient descent further.
There are many different landscapes in real-life problems, each requiring a special algorithm. Such algorithms are often two-level, with an algorithm choosing where to move in general at the top and another one solving a unimodal subproblem at the bottom. For example, an integer linear programming algorithm calls a continuous linear programming job as a sub-job and can do it again and again.

Non-unimodal job. Gradient descent may hit the wrong minimum.
A quantum computer is a system of n connected particles, each of which can be in one of two states. Therefore, the entire system has 2n states. In the common (non-quantum) world, we can say for sure that a particle is at this point with 100% probability and at another point with 0% probability.
In the quantum world, particles are in a superposition, which means that at the moment of measurement, the particle falls into one of two states with a certain probability. In the sum of the probabilities, superpositions of a particle make 100%, but we cannot know the exact state before we measure. A quantum particle can have different superposition variants with different probability distributions: 10/90, 50/50, or 70/30. This probability ratio is the quantum state of a particle and is represented by a circle with a radius of 1. A point on the circle with coordinates (x,y) is a superposition of a quantum particle with the probabilities of falling into the first state equal to x2, and into the second state equal to y2.
Thus, a quantum system is a lot of particles rotating in circles in different planes. When a quantum system is launched, the job statement and initial states of the particles are written into it, and all that stuff literally spins there. At the moment of measurement, it stops. Note that a quantum computer is made in such a way that the quantum system does not interact with anything and acts as a frictionless roulette that can spin forever. At the moment of measurement, the roulette stops. In the scientific language, this roulette is called Hamiltonian.
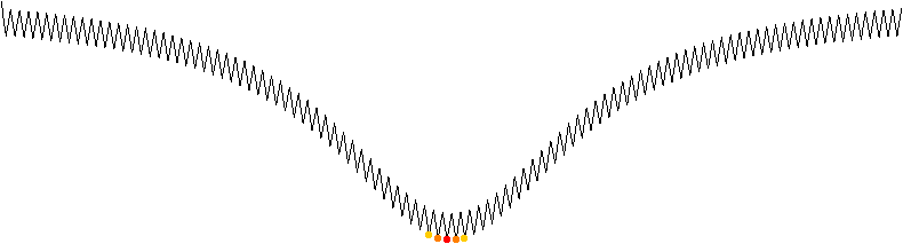
A typical combinatorial optimization job has many local minima, as well as many local minima that are close to the global one in value. Such jobs are challenging for both classical and quantum computers.
How is the correct answer found then? Each of the 2n variants matches its own area of the complex field of the roulette, and these areas have different sizes for different variants. The best answer corresponds to the maximum entropy, which, in turn, corresponds to the maximum area size. That is, when the roulette stops, this more often occurs in the area of the correct answer than in the area of the wrong one. However, this works well if there is exactly one best answer. But what if there are two or more? Well, it will be a challenge, a bunch of challenges. Although it is not completely clear how a quantum computer is to work, several scenarios can be envisioned:
- it will produce all relevant answers at some frequency;
- it will produce both the correct answers and some intermediate results, i.e. in addition to the areas related to the answers themselves, there will also present an intermediate "not very meaningful" area where the ball will roll. For example, if we have two optima 000…0 and 110…0, then in addition to these two answers, two more wrong results will be produced: 010…0 and 100…0.
- The results will "interfere", and the quantum computer will produce results that are far from the correct answers.
If the system has two different answers, then it will not stick with either point at a time but "run" from one to the other, and the answers will be confused. This explains the well-known Dzhanibekov effect. Any complex physical object (let it be a tennis racket) has two stable rotation axis. But any slight deviation from them makes movements look very confusing.
Given that even pulling out one answer is a probabilistic process, the existence of additional optima (optimal answers) will increase the time to result. And the more answers we have, the slower the quantum computer will work. Standard algorithms behave exactly the same way. So there may be a fundamental limit to the quantum computer operation, unknown to science so far.
Similarly, local minima, which slightly differs from global ones, will hinder the operation. To worsen the situation, a non-trivial optimization problem will have a lot of local minima.
In short, a quantum computer will cope with non-unimodal jobs, but hardly.
Summing up, a quantum computer is like Buridan's donkey. It can easily choose from many haystacks if there is the most prominent and most delicious among them but starve when placed in the middle between two identical ones.
Thus, we have discovered the fundamental property of a quantum computer (not faced yet): it solves a problem well if there is exactly one answer.
So, quantum computers will hardly contribute to a dramatic breakthrough in solving practical optimization problems soon.